Rumus abc Persamaan Kuadrat

Ada beberapa cara yang dapat digunakan untuk mencari suku/faktor nilai $x$ pada persamaan kuadrat, misalnya menggunakan pemfaktoran, melengkapkan bentuk kuadrat, maupun menggunakan rumus kuadrat atau biasa juga disebut rumus abc. Untuk persamaan kuadrat $ax^2 + bx + c = 0$ dengan nilai $a>1$ ataupun bentuk persamaan kuadrat yang sulit difaktorkan, biasanya akan lebih mudah diselesaikan jika menggunakan rumus kuadrat, yaitu $x_1,_2 = \frac {- b \pm \sqrt{b^2 - 4ac}}{2a}$ . Pada postingan kali ini akan dibahas bagaimana cara memperoleh rumus abc tersebut.

Bentuk umum dari persamaan kuadrat adalah $ax^2 + bx + c = 0$

$\Leftrightarrow ax^2 + bx = -c$

$\Leftrightarrow x^2 + \frac {b}{a}x = -\frac {c}{a}$

$\Leftrightarrow x^2 + \frac {b}{a}x + (\frac {b}{2a})^2 = (\frac {b}{2a})^2 - \frac {c}{a}$

$\Leftrightarrow (x + \frac {b}{2a})^2 = (\frac {b}{2a})^2 - \frac {c}{a}$

$\Leftrightarrow (x + \frac {b}{2a})^2 = \frac {b^2}{4a^2} - \frac {4ac}{4a^2}$

$\Leftrightarrow x + \frac {b}{2a} = \pm \sqrt \frac {b^2-4ac}{4a^2}$

$\Leftrightarrow x = -\frac {b}{2a} \pm \frac {\sqrt {b^2 - 4ac}}{2a}$

$\Leftrightarrow x= \frac {- b \pm \sqrt {b^2 - 4ac}}{2a}$

$x_1 = \frac {- b + \sqrt{b^2 - 4ac}}{2a}$ dan $x_2 = \frac {- b - \sqrt{b^2 - 4ac}}{2a}$

Dengan rumus tersebut kita akan lebih mudah dalam mencari akar-akar persamaan kuadrat dengan bentuk $ax^2 + bx + c =0$ , kita tinggal memasukkan nilai-nilai $a, b,$ dan $c$ ke dalam rumusnya.

Secara umum persamaan kuadrat berbentuk ax2 + bx + c = 0 dengan a 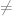$\neq$ 0. Persamaan kuadarat seperti ini memiliki tiga bentuk akar-akar persamaan, yaitu memiliki dua akar riil dan berbeda (jika D > 0), memiliki dua akar riil dan sama (jika D < 0) dan tidak memiliki akar riil atau biasa dikenal dengan tidak memiliki solusi (jika D < 0). Apa D? D adalah singkatan dari Diskriminan yaitu memiliki rumus D = $\sqrt{b^2-4ac}$ .